Solving PDEs, Inverse Problems in Geophysics, Quantum Mechanics, Multi-phase Flow, and Optics
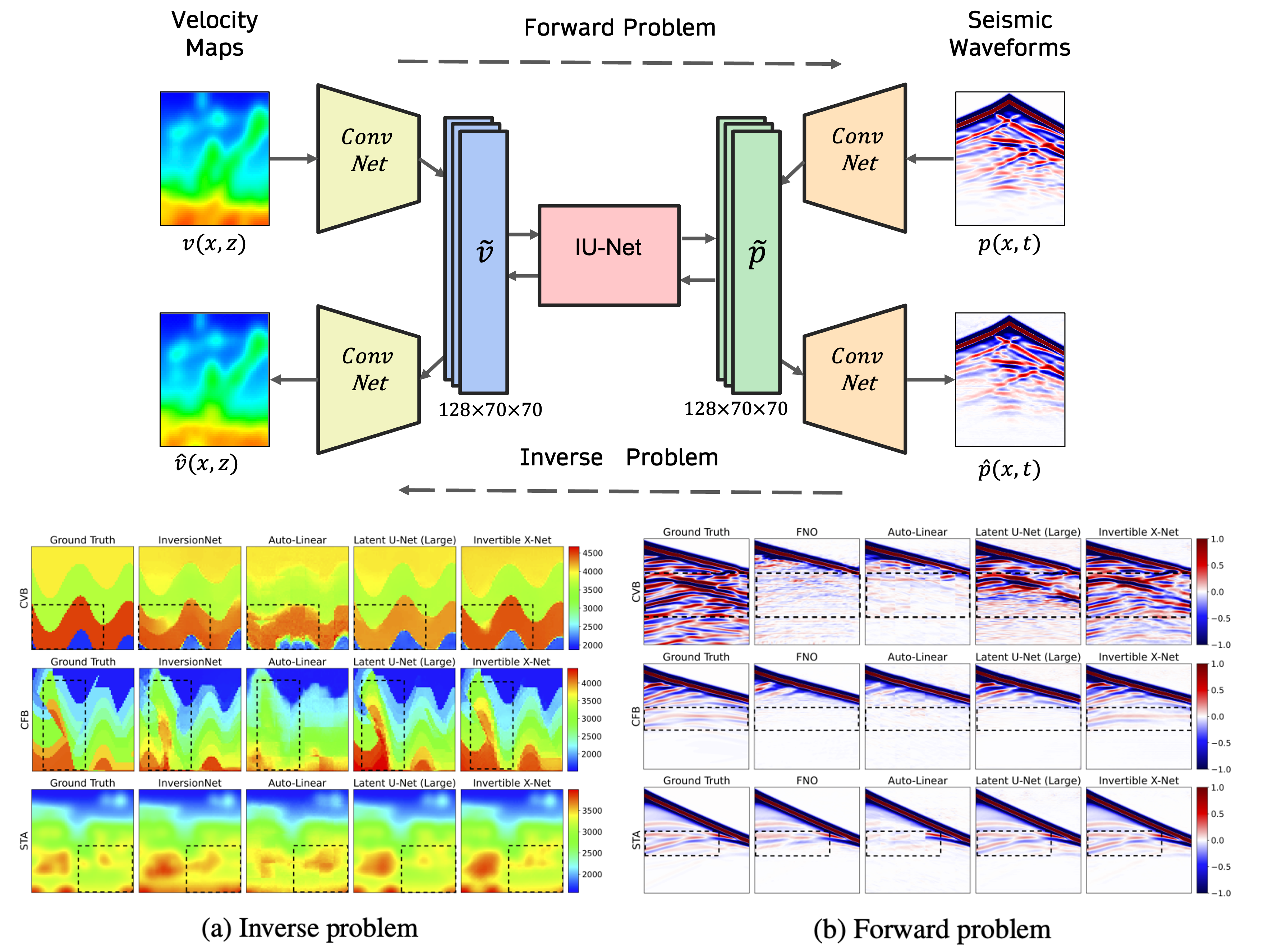
This is a collaborative project with computer scientists and physicists from Virginia Tech, Ohio State University, SUNY Bingamton, and University of Massachusetts Lowell. The goal of this project is to train neural network models for solving eigenvalue equations in physics problems (Schrodinger’s equation in quantum mechanics and Maxwell’s equations in optics) using physics-guided learning algorithms. We are also developing neural network architectures and learning algorithms for solving PDEs using limited number of ground-truth simulations and multi-phase flow problems. We are exploring ideas from several fields to improve the parameter efficiency, convergence speed, and generalization capabilities of neural networks, especially on out-of-distribution samples. This work has been supported by an NSF EAGER grant we received in 2020.
Papers: